RSLogix 5000 PID Tuning

What do you know about tuning a PID loop in RSLogix 5000?

When it comes to PID loops and tuning first you have to understand what each element is in the loop. Proportional, Integral, Derivative are the main components of the standard PID loop. Proportional is often shown as the symbol Kp while Integral is shown as Ki and the Derivative being shown as the symbol Kd. As these are the main elements of the PID as in the name, the next very important parts are the update time, the control variable, and the error of the loop.

PID is short for:

• Kp
• Ki
• Kd

There are a few examples in this article so that I can show how diverse the PID instruction is. Whether you have a system that requires very simple control over a process like a tank level control or a more aggressive control application like a mixing system such as a batch-making station.

PID Loop Timing 

The PID instruction and the sampling of the process variable need to be updated at a periodic rate. This update time is related to the physical process you are controlling. For very slow loops, such as temperature loops, an update time of once per second or even longer is usually sufficient to obtain good control.

Somewhat faster loops, such as pressure or flow loops, may require an update time such as once every 250ms. Only rare cases, such as tension control on an unwinder spool, require loop updates as fast as every 10ms or faster. Because the PID instruction uses a time base in its calculation, you need to synchronize the execution of this instruction with the sampling of the process variable (PV ).

The easiest way to execute the PID instruction is to put the PID instruction in a periodic task. Set the loop update time (.UPD) equal to the periodic task rate and make sure that the PID instruction is executed every scan of the periodic task.

When using a periodic task, make sure that the analog input used for the process variable is updated to the processor at a rate that is significantly faster than the rate of the periodic task. Ideally, the process variable should be sent to the processor at least five to 10 times faster than the periodic task rate.

This minimizes the time difference between actual samples of the process variable and the execution of the PID loop. For example, if the PID loop is in a 250 ms periodic task, use a loop update time of 250 ms (.UPD = .25), and configure the analog input module to produce data at least about every 25 to 50 ms. Another, somewhat less accurate, method of executing a PID instruction is to place the instruction in a continuous task and use a timer done a bit to trigger execution of the PID instruction.

Shown in the video below, I use a timer and a simple setup with a trend to show a slow method of tuning and also a faster method of tuning.

As you can see in the video I made above, the use of a trend in tuning a PID loop is just about the only way to accurately tune one and get it to respond to whatever application you have.

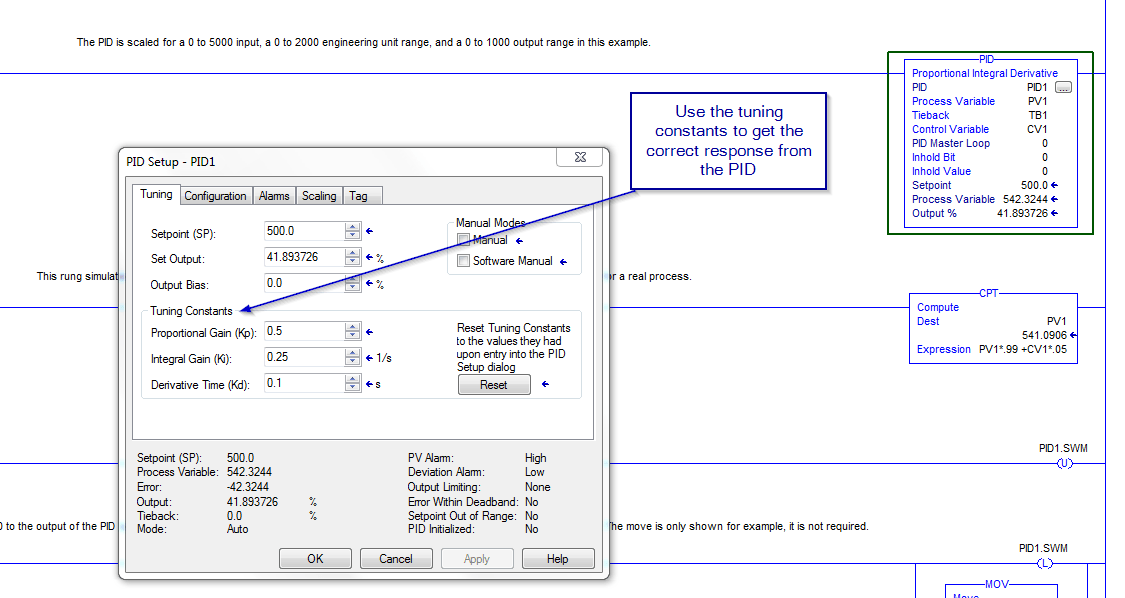
You can tune a system fast or slow, it really just depends on your application and what time of loop you are controlling. Using the tuning constants is what will lead your system to get the proper response no matter what type of application you are set up for.

In the video, it is shown a simple setup to give you the most detail that can be given in a short video with no question and answer type setup. The tags of the PID are made to fit the part of the instruction that is needed instead of having different names.

Therefore, if a PID is used, the tag is PID1 and if a Process Variable is used then it is PV1, and so on. This gives a very simple setup to limit confusion about tag names and such.

To tune the PID loop, use the proportional gain, the Integral Gain, and the Derivative Time. You can see in the video, how each of these work and why you would change each of these to give a slow response or a fast response.

You can also use the bits of the PID instruction to control the action of the loop, let’s say that you want to be able to through the PID control in manual at times and then back into an auto at other times. then you can use the .swm bit as shown in the below picture.

PID closed-loop control holds a process variable at the desired set point.

Shown below is a flow-rate/fluid level example:

In the above example, the level in the tank is compared against the setpoint. If the level is higher than the setpoint, the PID equation increases the control variable and causes the outlet valve from the tank to open; thereby decreasing the level in the tank.

The PID equation used in the PID instruction is a positional form equation with the option of using either independent gains or dependent gains. When using independent gains, the proportional, integral, and derivative gains only affect their specific proportional, integral, or derivative terms respectively.

When using dependent gains, the proportional gain is replaced with a controller gain which affects all three terms. You can use either form of the equation to perform the same type of control. The two-equation types are merely provided to let you use the equation type with which you are most familiar.

Rockwell Automation PID Support Document

Visit: Allen-Bradley-PLC-Training

Or visit my YouTube channel at:

What do you know about tuning a PID loop in RSLogix 5000?

When it comes to PID loops and tuning first you have to understand what each element is in the loop. Proportional, Integral, Derivative are the main components of the standard PID loop. Proportional is often shown as the symbol Kp while Integral is shown as Ki and the Derivative being shown as the symbol Kd. As these are the main elements of the PID as in the name, the next very important parts are the update time, the control variable, and the error of the loop.

PID is short for:

• Kp
• Ki
• Kd

There are a few examples in this article so that I can show how diverse the PID instruction is. Whether you have a system that requires very simple control over a process like a tank level control or a more aggressive control application like a mixing system such as a batch-making station.

PID Loop Timing 

The PID instruction and the sampling of the process variable need to be updated at a periodic rate. This update time is related to the physical process you are controlling. For very slow loops, such as temperature loops, an update time of once per second or even longer is usually sufficient to obtain good control.

Somewhat faster loops, such as pressure or flow loops, may require an update time such as once every 250ms. Only rare cases, such as tension control on an unwinder spool, require loop updates as fast as every 10ms or faster. Because the PID instruction uses a time base in its calculation, you need to synchronize the execution of this instruction with the sampling of the process variable (PV ).

The easiest way to execute the PID instruction is to put the PID instruction in a periodic task. Set the loop update time (.UPD) equal to the periodic task rate and make sure that the PID instruction is executed every scan of the periodic task.

When using a periodic task, make sure that the analog input used for the process variable is updated to the processor at a rate that is significantly faster than the rate of the periodic task. Ideally, the process variable should be sent to the processor at least five to 10 times faster than the periodic task rate.

This minimizes the time difference between actual samples of the process variable and the execution of the PID loop. For example, if the PID loop is in a 250 ms periodic task, use a loop update time of 250 ms (.UPD = .25), and configure the analog input module to produce data at least about every 25 to 50 ms. Another, somewhat less accurate, method of executing a PID instruction is to place the instruction in a continuous task and use a timer done a bit to trigger execution of the PID instruction.

As shown in the video below, I use a timer and a simple setup with a trend to show a slow method of tuning and also a faster method of tuning.

As you can see in the video I made above, the use of a trend in tuning a PID loop is just about the only way to accurately tune one and get it to respond to whatever application you have.

You can tune a system fast or slow, it really just depends on your application and what time of loop you are controlling. Using the tuning constants is what will lead your system to get the proper response no matter what type of application you are set up for.

In the video, it is shown a simple setup to give you the most detail that can be given in a short video with no question and answer type setup. The tags of the PID are made to fit the part of the instruction that is needed instead of having different names.

Therefore, if a PID is used, the tag is PID1 and if a Process Variable is used then it is PV1, and so on. This gives a very simple setup to limit confusion about tag names and such.

To tune the PID loop, use the proportional gain, the Integral Gain, and the Derivative Time. You can see in the video, how each of these work and why you would change each of these to give a slow response or a fast response.

You can also use the bits of the PID instruction to control the action of the loop, let’s say that you want to be able to through the PID control in manual at times and then back into auto in other times. then you can use the .swm bit as shown in the below picture.

PID closed-loop control holds a process variable at the desired set point.

Shown below is a flow-rate/fluid level example:

In the above example, the level in the tank is compared against the setpoint. If the level is higher than the setpoint, the PID equation increases the control variable and causes the outlet valve from the tank to open; thereby decreasing the level in the tank.

The PID equation used in the PID instruction is a positional form equation with the option of using either independent gains or dependent gains. When using independent gains, the proportional, integral, and derivative gains only affect their specific proportional, integral, or derivative terms respectively.

When using dependent gains, the proportional gain is replaced with a controller gain which affects all three terms. You can use either form of the equation to perform the same type of control.

The two equation types are merely provided to let you use the equation type with which you are most familiar.

Rockwell Automation PID Support Document

Visit: Allen-Bradley-PLC-Training

Again, I hope you were able to pick up some good learning and please let me know what topics that you are interested in for further articles.

Or visit my YouTube channel at:

Below I have put together a small list of helpful articles to aid you in future searches or for now if you happen to have time, I do recommend you bookmark this site or follow my YouTube channel to help you stay up with our current topics.

More PLC Topics

FactoryTalk SE HMI

• FactoryTalk SE HMI Restore And Emulate

• FactoryTalk View HMI Anti-Sticky Button

• FactoryTalk Studio HMI Client Startup Macro

FactoryTalk SE HMI

FactoryTalk SE HMI Restore And Emulate

FactoryTalk View HMI Anti-Sticky Button

FactoryTalk Studio HMI Client Startup Macro